| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 자바강좌
- 파이썬강의
- acmicpc.net
- 효묘블로그
- 머신러닝 강의
- 자바시작하기
- 경사하강법
- c언어 오목
- 딥러닝
- 자바
- 코딩테스트
- feature scaling
- 머신러닝
- python강좌
- 비지도학습
- JAVA강좌
- 머신러닝 강좌
- unsupervised learning
- 딥러닝공부
- java
- 선형회귀
- Python강의
- 파이썬강좌
- supervised learning
- 지도학습
- 백준 알고리즘
- 인공지능
- 머신러닝공부
- Gradient Descent
- 비용함수
- Today
- Total
컴공과컴맹효묘의블로그
백준[1395] 스위치 본문
https://www.acmicpc.net/problem/1395
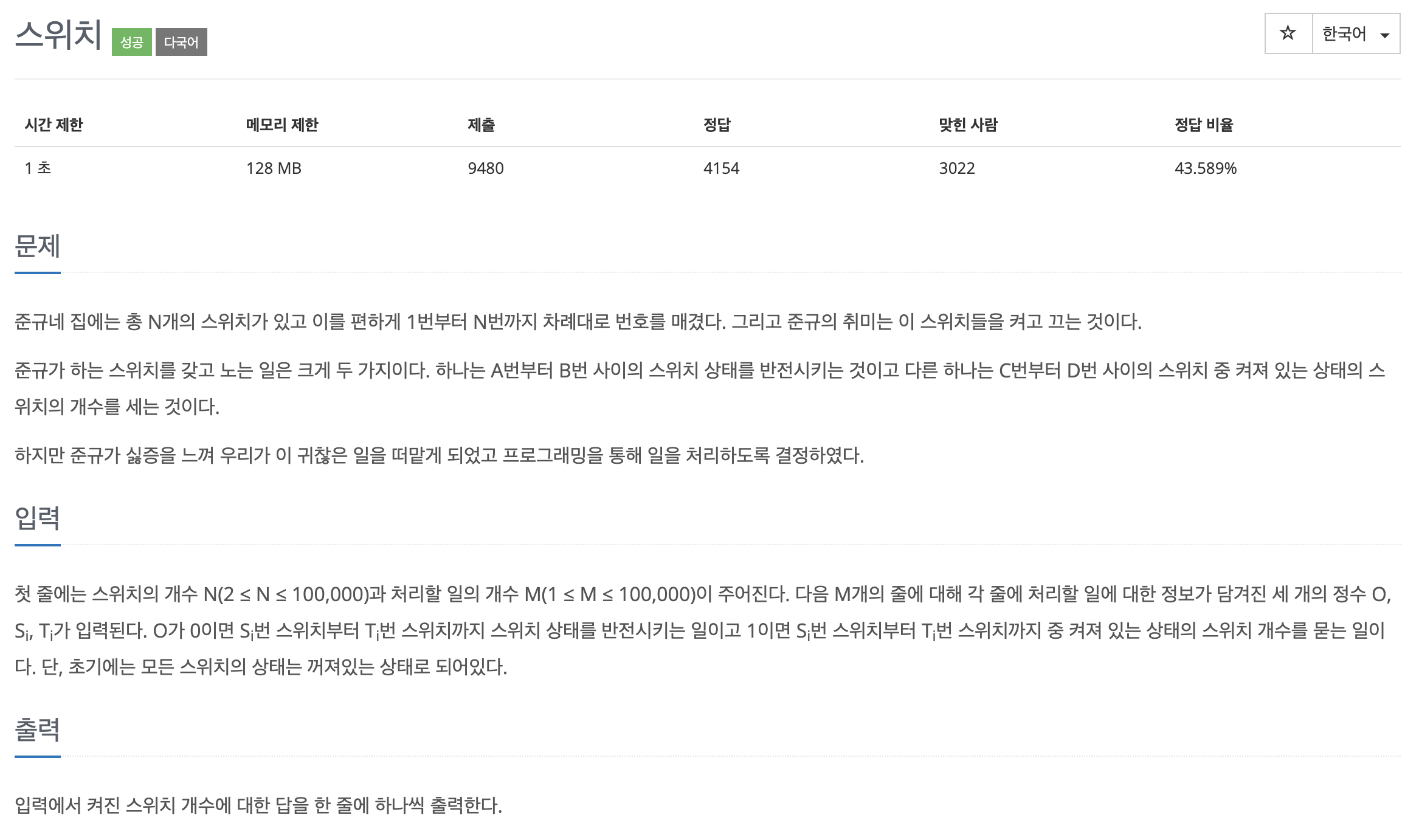
이 문제는 특정 구간을 스위치하거나, 특정 구간의 켜진 스위치의 합을 구하는 문제이다.
구간합 문제로 생각했고, segment tree를 최적화하면 풀 수 있다고 생각했다.
하지만 최적화를 위한 아이디어를 바로 떠올리긴 어려웠다.
일반적인 segment tree에서 단일 원소 갱신은 $log{N}$이므로 단순 구간 갱신은 $N log{N}$이 될 것이다.
다른 방법을 찾아봐야한다.
처음엔 각 원소가 0과 1을 갖는 단순한 특징 때문에 단순히 특정한 수학적 연산으로 가능할 줄 알았다. 그렇게 해서 떠올린 것의 시간복잡도는 결국 $log^2N$이었다.
결국 인터넷에서 답을 찾았고 lazy segment tree 아이디어를 사용해야했다.
아이디어는 이렇다.
구간 합을 구할 때 모든 노드를 조회하지 않는다. 예를 들어 5~8 구간을 조회해야한다면 해당 노드를 그냥 반환하면 된다. 그 노드에는 이미 위치 5~8에 해당하는 합이 존재하니까.
lazy segment tree는 특정 노드가 가지는 구간을 전부 업데이트 (예를 들어 구간 1~8을 업데이트할 때 노드5~8를 탐색하여 업데이트를 하는 경우)할 때 해당 노드의 자식 노드를 탐색 보류하는 것이다.
합을 구할 때는 해당 노드를 반환해주면 되고, 자식 노드는 굳이 탐색할 필요가 없기 때문이다.
그렇다면 "자식 노드 업데이트 예정"이라는 것을 어딘가에 적어둘 변수가 필요하다.
변수 또한 tree로 만들고 보통 lazy라는 변수명을 사용한다.
그리고 구간 갱신과 구간 합 함수를 호출할 때 lazy를 업데이트해주면 된다.
#include <iostream>
#include <iomanip>
#include <algorithm>
#include <vector>
#include <queue>
#include <math.h>
#include <map>
#include <climits>
#include <set>
#include <string>
#define INF 987654321
#define MAX_N 100000
#define lld long long int
using namespace std;
int N, M;
int tree[MAX_N*4];
int lazy[MAX_N*4];
inline void updateLazy(int start, int end, int n) {
if(lazy[n] % 2 == 1) {
tree[n] = (end - start + 1) - tree[n]; // update
if(start != end) {
lazy[n*2] += lazy[n];
lazy[n*2+1] += lazy[n];
}
lazy[n] = 0;
}
}
int query(int start, int end, int n, int left, int right) {
updateLazy(start, end, n);
if(right < start || left > end) return 0;
if(left <= start && end <= right) return tree[n];
int mid = (start+end) / 2;
return
query(start, mid, n*2, left, right) +
query(mid+1, end, n*2+1, left, right);
}
void update(int start, int end, int n, int left, int right) {
updateLazy(start, end, n);
if(right < start || left > end) return;
if(left <= start && end <= right) { // completely inside
tree[n] = (end - start + 1) - tree[n]; // switch
if(start != end) { // if not a leaf node
// lazy update for children
lazy[n*2] += 1;
lazy[n*2+1] +=1;
}
return;
}
int mid = (start + end) / 2;
update(start, mid, n*2, left, right);
update(mid+1, end, n*2+1, left, right);
tree[n] = tree[n*2] + tree[n*2+1];
return;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
cin >> N >> M;
for(int i = 0; i < M; i++) {
int c, a, b;
cin >> c >> a >> b;
if(c == 0) {
update(0, N-1, 1, a-1, b-1);
} else {
cout << query(0, N-1, 1, a-1, b-1) << '\n';
}
}
return 0;
}'알고리즘 > 백준' 카테고리의 다른 글
| 백준[1086] 박상원 (0) | 2025.10.01 |
|---|---|
| 백준[11066] 파일 합치기 (0) | 2025.05.11 |
| 백준[1725] 히스토그램 (0) | 2025.05.05 |
| 백준[1241] 머리 톡톡 (0) | 2025.05.04 |
| 백준[2230] 수 고르기 (0) | 2022.07.24 |



