| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 비용함수
- 지도학습
- JAVA강좌
- 백준 알고리즘
- 선형회귀
- 파이썬강좌
- feature scaling
- 파이썬강의
- 코딩테스트
- acmicpc.net
- supervised learning
- Python강의
- 자바강좌
- c언어 오목
- 효묘블로그
- 인공지능
- 딥러닝
- 자바시작하기
- java
- 비지도학습
- 자바
- 머신러닝공부
- 머신러닝
- 머신러닝 강좌
- unsupervised learning
- 경사하강법
- python강좌
- Gradient Descent
- 머신러닝 강의
- 딥러닝공부
- Today
- Total
컴공과컴맹효묘의블로그
이분 매칭 알고리즘 C++ 그림 설명 (Bipartite Matching) 본문
백준 문제를 풀던 도중 이분 매칭 알고리즘이라는 것을 처음 접했다.
두 집합에 대해서 서로가 매칭할 수 있는 간선이 있을 때, 겹치지 않고 최대로 많은 매칭을 구하는 것이다.
정확히 말해 이분 그래프에 대해서 각 정점이 하나의 간선만 소유하는 것.
DFS를 사용하면 O(VE), Hopcroft-Karp알고리즘을 사용하면 O(sqrt(V)E)이다.
처음에 이해가 잘 가지 않아서 코드와 그림을 step by step으로 이해하며 분석했다.
해당 알고리즘은 다음과 같다.
현재 노드가 연결할 수 있는 노드에 연결했을 때 이전에 매칭된 노드들을 끊어지지 않게 재배치할 수 있다면 현재 노드의 연결을 허용한다. 만약 재배치가 불가능하다면, 현재 노드가 연결할 수 있는 또다른 노드를 찾아 위를 반복한다.
각 노드에 대해서 반복한다.
- 연결 가능한 노드에 방문할 것.
- 연결 가능하면 연결하고, 누가 점유하고 있으면 해당 점유자에 대해서 방문한 노드를 제외하고 위 과정을 반복할 것. (해당 점유가자 다른 노드에 연결할 수 있는지 확인한다는 것.)
- 연결이 불가능하면 해당 노드는 연결 불가능함.
따라서 필요한 추가적인 변수는 방문 노드(visited 혹은 done)와 점유 노드(slt슬롯을 뜻함)이다.
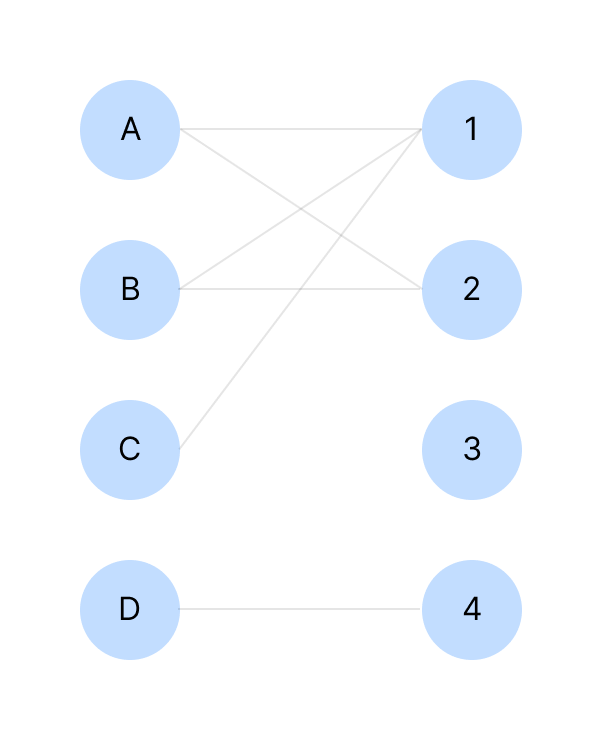
위와 같은 매칭 노드가 있다고 해보자.
A에 대해서 탐색한다.
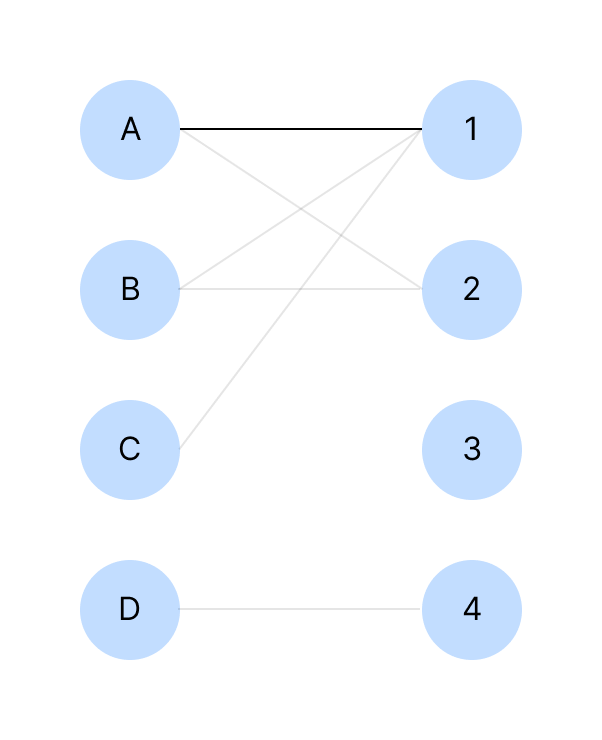
A는 1에 연결 가능하다. 이제 B에 대해서 탐색한다.
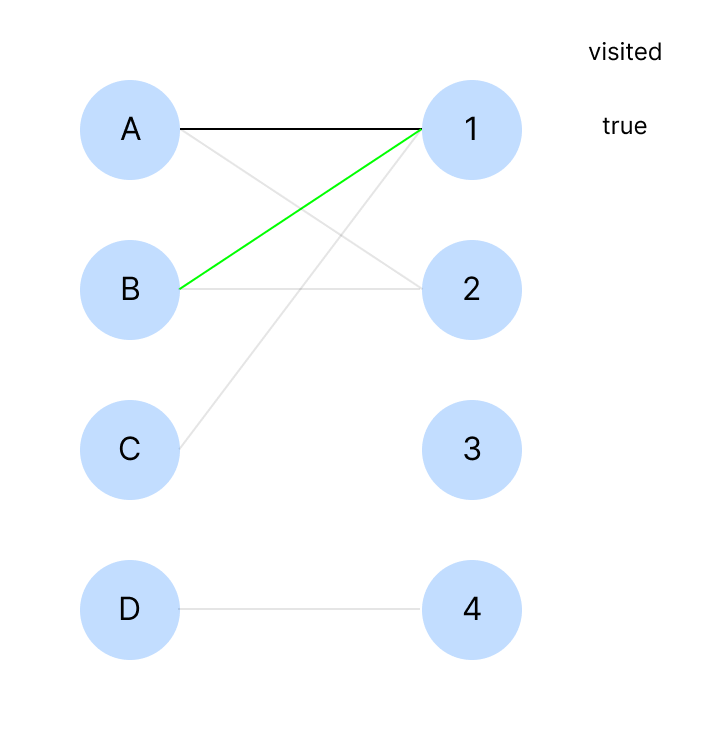
B는 1에 연결할 수 있다. 하지만, 1은 A에 의해 점유된다.
따라서 A에 대해 탐색(dfs)을 시작한다.
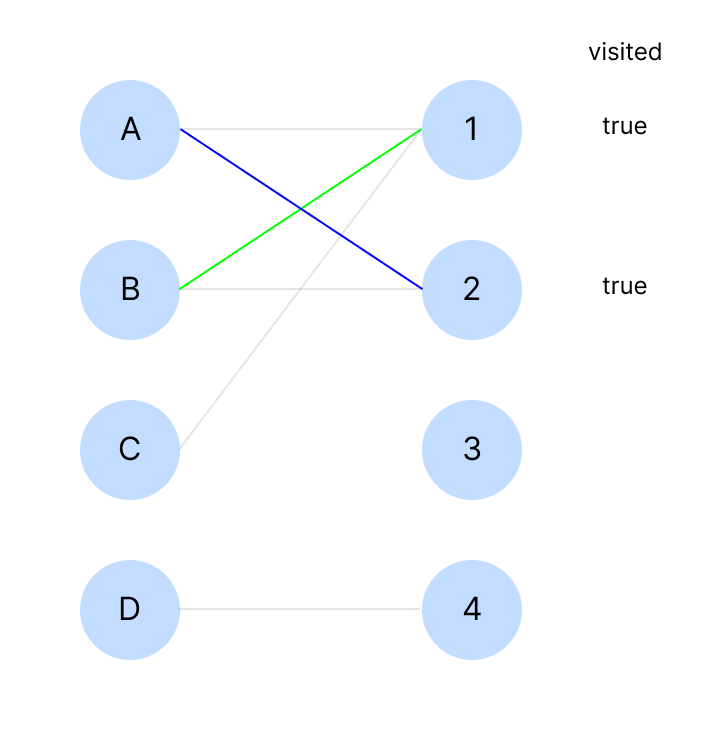
A는 방문하지 않은 노드 중 다음 노드인 2를 탐색한다.
연결 가능하여 A와 2를 매칭한다.
A가 매칭에 성공하여 B는 이제 1과 연결할 수 있으니 연결한다.
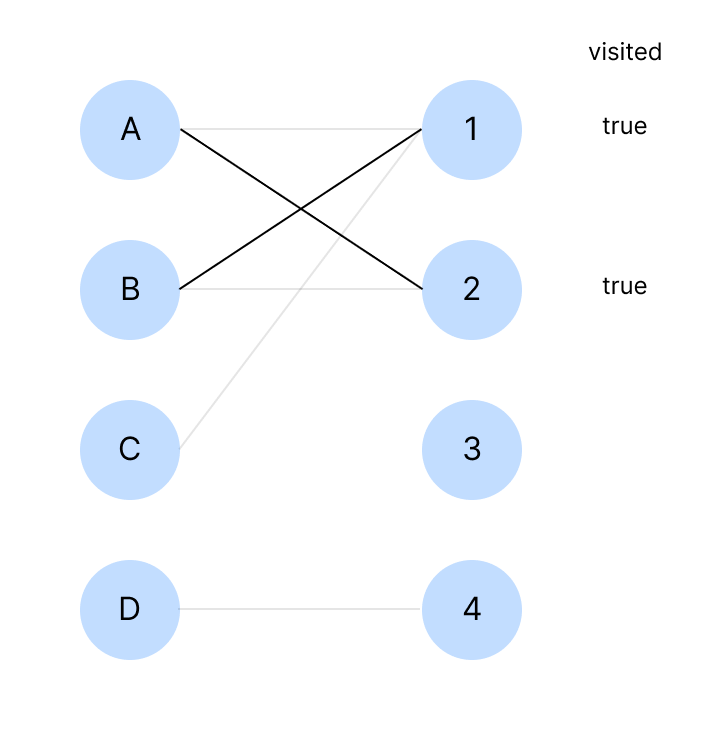
C에 대해서 탐색한다.
C는 1에 연결할 수 있다.
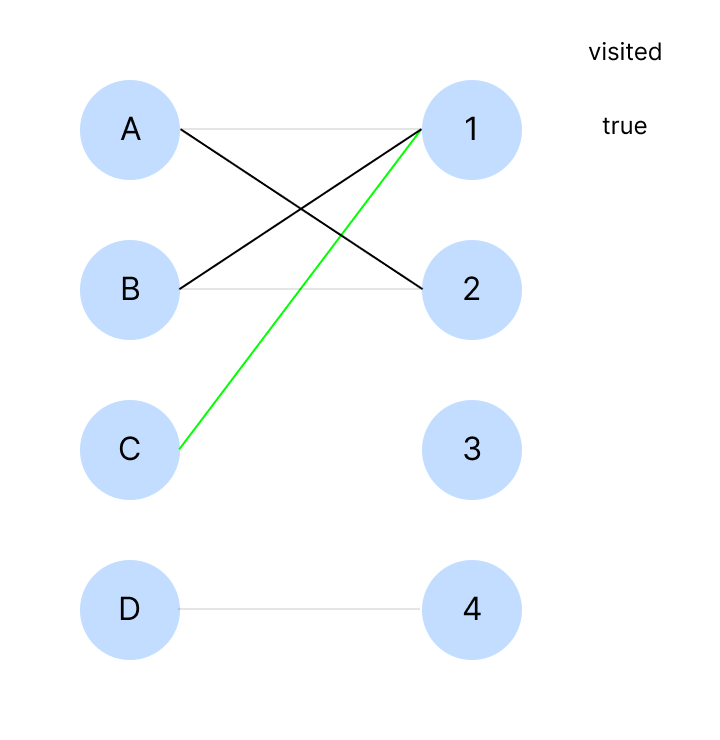
1을 점유하는 B가 존재하기 때문에 B에 대해서 탐색(dfs) 한다.
B는 2와 연결할 수 있다. 하지만 2는 A가 점유하고 있으니 A에 대해 탐색(dfs) 한다
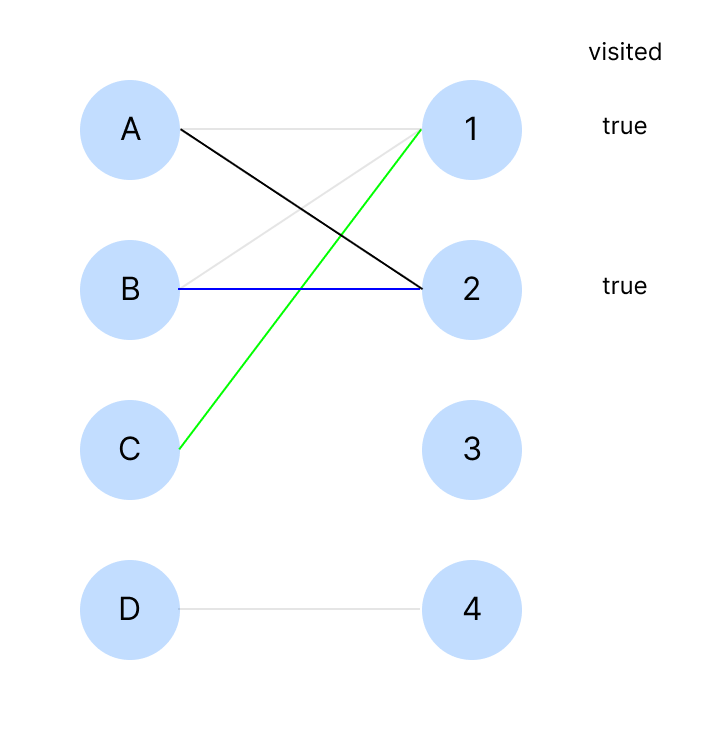
A는 이제 연결할 수 있는 노드가 없기 때문에 탐색을 종료한다.
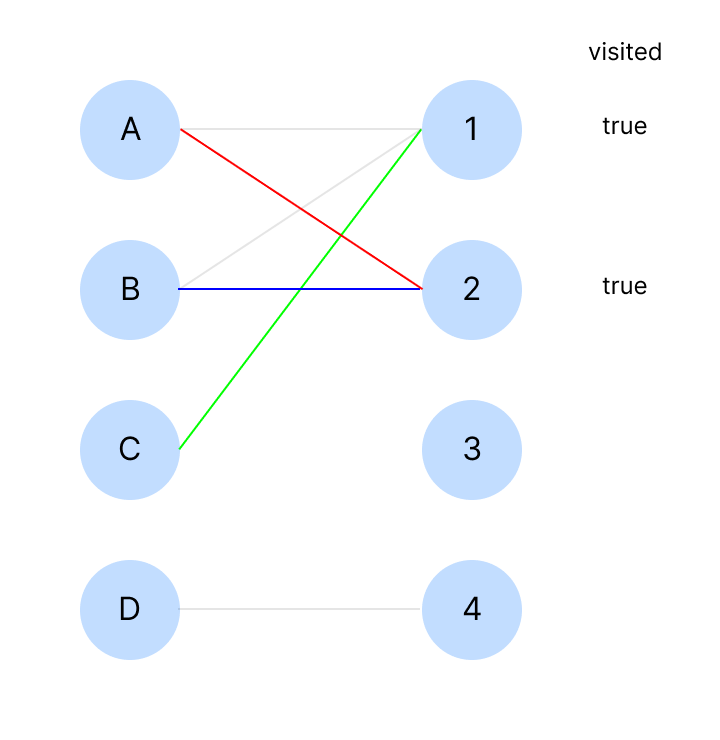
C는 다음 연결 노드를 찾는다. 하지만 존재하지 않으므로 탐색을 종료하고 false를 리턴한다.
main의 dfs가 false이므로 cnt가 증가하지 않는다.
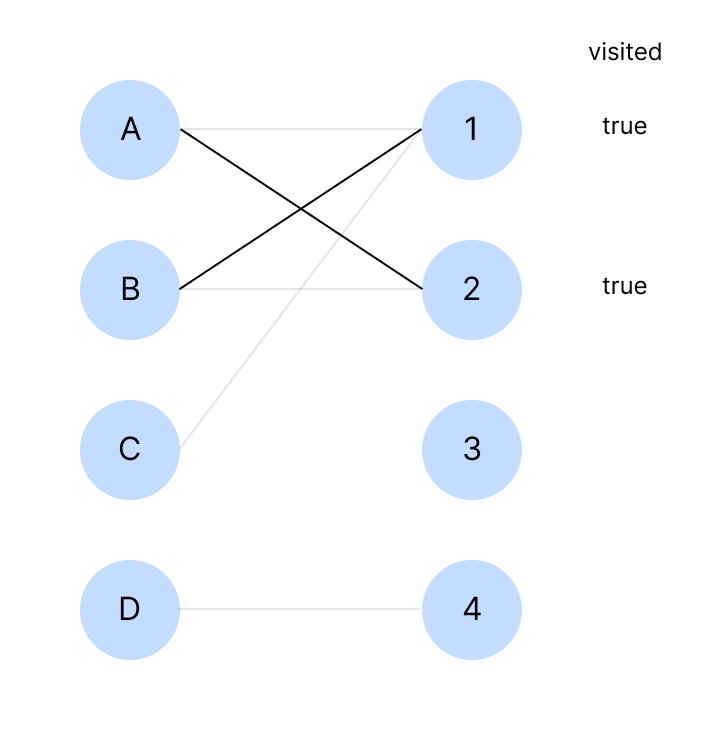
마지막으로 D는 4와 연결된다.
// ...
int N, M, K;
vector<int> adj[MAX_N];
bool done[MAX_N];
int slt[MAX_N];
bool dfs(int x) {
for(int i = 0; i < adj[x].size(); i++) {
int p = adj[x][i];
if(done[p]) continue;
done[p] = true;
if(slt[p] == 0 || dfs(slt[p])) {
slt[p] = x;
return true;
}
}
return false;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);cout.tie(NULL);
int n = 4;
int cnt = 0;
adj[1].push_back(1);
adj[1].push_back(2);
adj[2].push_back(1);
adj[2].push_back(2);
adj[3].push_back(1);
adj[4].push_back(4);
for(int i = 1; i <= n; i++) {
fill(done, done+n, false);
if(dfs(i)) {
cnt++;
}
}
cout << "Total matching count: " << cnt << endl;
for(int i = 1; i <= n; i++) {
cout << slt[i] << " -> " << i << endl;
}
return 0;
}
결과
Total matching count: 3
2 -> 1
1 -> 2
0 -> 3
4 -> 4
0 -> 5'알고리즘 > 알고리즘 교양' 카테고리의 다른 글
| 카카오 코드 페스티벌 2018 본선 문제(백준) (0) | 2020.06.29 |
|---|

