| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- java
- python강좌
- 머신러닝 강좌
- 머신러닝공부
- 자바시작하기
- 파이썬강좌
- 머신러닝
- c언어 오목
- 경사하강법
- acmicpc.net
- 파이썬강의
- 지도학습
- 인공지능
- 머신러닝 강의
- unsupervised learning
- 선형회귀
- 자바강좌
- 자바
- 코딩테스트
- 백준 알고리즘
- supervised learning
- 비지도학습
- JAVA강좌
- 딥러닝공부
- feature scaling
- Gradient Descent
- 딥러닝
- 효묘블로그
- Python강의
- 비용함수
- Today
- Total
컴공과컴맹효묘의블로그
수알못의 머신러닝 공부 : 비용함수 본문
안녕하세요, 효묘입니다. 요즘 앤드류 응 교수님의 강의를 들으면서 배운 내용을 블로그에 기록해보려고 합니다.
첫 번째로 쓸 내용은 비용함수입니다.
Cost function
경제학에서, 비용함수는 어떤 생산량에서의 최소 생산비용을 대응한 함수이다. 이를 그림으로 나타낸 그래프를 비용곡선이라 한다. 고정 생산요소의 존재여부에 따라 장기와 단기 비용곡선을 나누며, 총비용함수 TC=TC(Q) 에서 한계비용함수와 평균비용함수를 유도한다.-wikipedia
위키피디아에서 뜻을 검색해봤는데 잘 모르겠네요.
아무튼 제가 이해한 방식으로 설명 해보겠습니다.
제가 서울에서 택시를 타고 이동하려고 합니다. 이때, 택시의 거리에 따른 값의 그래프를 그려보겠습니다.
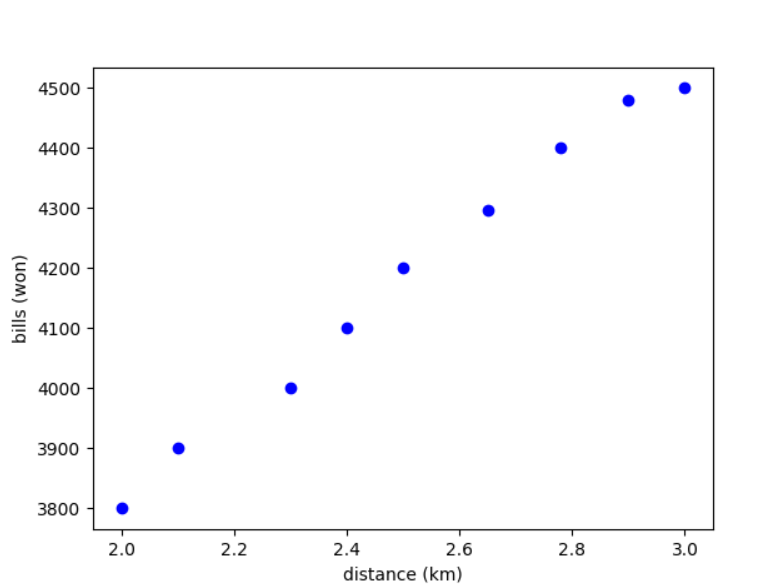
거리에따른 택시 요금의 실제 데이터라고 가정합시다. 이 데이터는 걸린 시간을 가정하지 않았습니다. 따라서 그래프의 점들이 균일하지 않습니다.
이 그래프와 제일 잘 맞는 직선을 하나 그려보겠습니다.
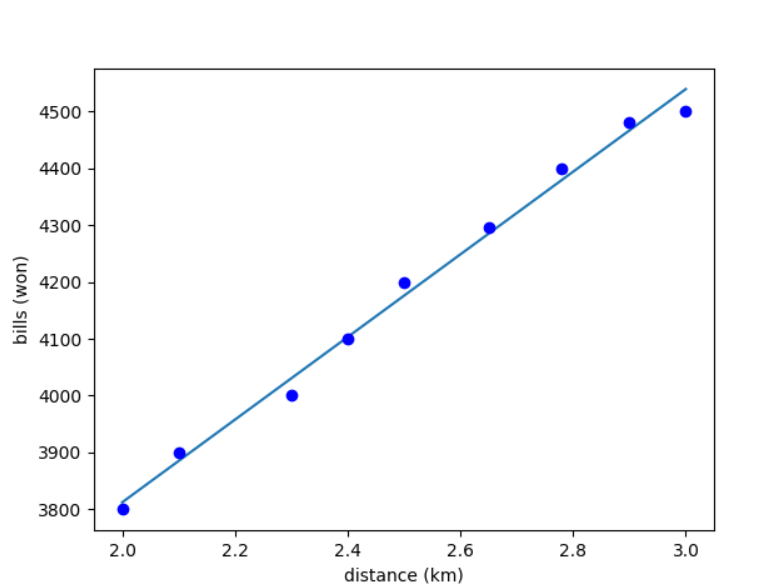
모든 점들을 지나지는 않지만, 가장 잘 맞는 직선이라하면 맞을겁니다. 이 직선을 다음과 같이 표현하겠습니다.
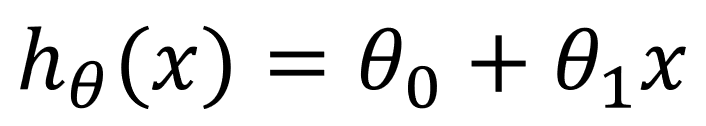
그리고 저 점들과 이 직선이 완전히 일치하지는 않기때문에 오차가 발생할 겁니다.
이러한 오차를 표현하는 함수를 비용함수라고 합니다.
오차함수를 표현하기 전에 몇 가지 기호를 정하고 가겠습니다.
m은 총 학습 데이터의 개수,
i는 학습 데이터가 몇 번째인지 표현하는 기호입니다.
오차는 다음과 같이 표현됩니다.
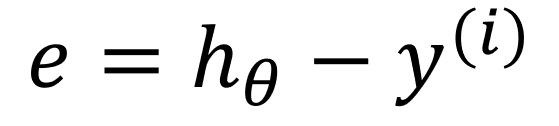
e는 그냥 뺀 것이니, 거리를 구하려면 절댓값을 씌워줘야 합니다.
하지만 절댓값을 씌워주면, 미분 불능점이 나올 수 있기 때문에 제곱을 해줍니다.
그리고 모든 학습데이터를 더한 후에, 제곱의 평균을 구해야하니 m으로 나눕니다.
그리고, 미분하면 2가 떨어지니까 1/2를 한번 더 곱합니다.
그럼 다음과 같은 식을 표현할 수 있습니다.
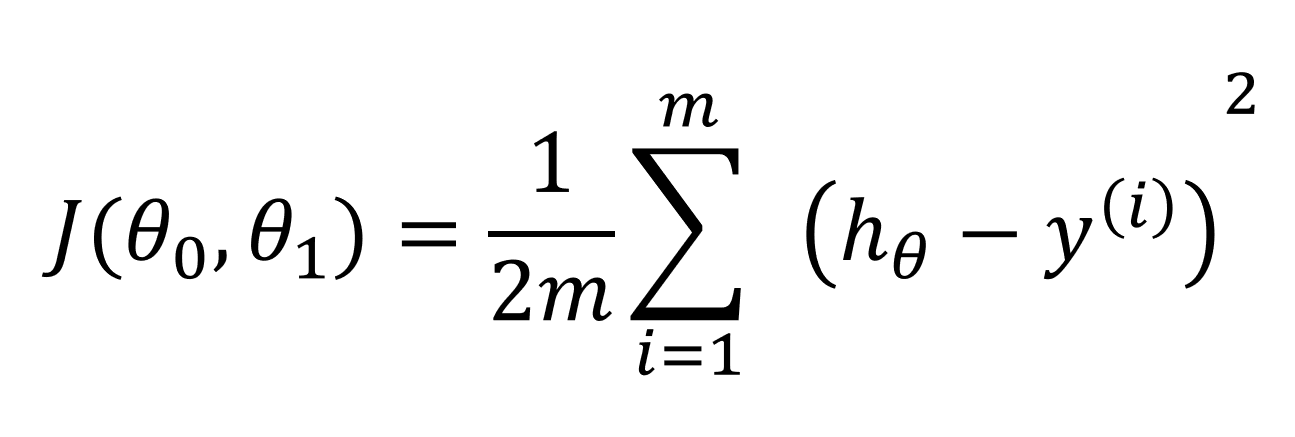
이때 J를 비용함수 Cost function이라고 합니다.
비용함수를 한 문장으로 표현하자면, "오차를 표현해주는 미분 가능한 함수"라고 할 수 있겠습니다.
이제 이 비용함수의 최솟값을 구하면 거리에 따른 택시요금을 가장 잘 구할 수 있는 직선을 구할 수 있을겁니다.
이러한 방식을 선형회귀(linear regression)라고도 부릅니다.
'컴퓨터 > 머신러닝' 카테고리의 다른 글
| 수알못의 머신러닝 공부 : 행렬과 벡터_행렬곱 (0) | 2019.06.27 |
|---|---|
| 수알못의 머신러닝 공부 : 행렬과 벡터_표현 (0) | 2019.06.25 |
| 수알못의 머신러닝 공부 : 경사하강법 Python으로 구현해보기 (0) | 2019.06.18 |
| 수알못의 머신러닝 공부 : 경사하강법 (0) | 2019.06.17 |
| 머신러닝 기초 : 머신러닝이란? (0) | 2019.06.16 |





