| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 비용함수
- 경사하강법
- 코딩테스트
- python강좌
- 인공지능
- supervised learning
- Python강의
- Gradient Descent
- 머신러닝
- 자바강좌
- 파이썬강의
- 딥러닝공부
- 선형회귀
- 파이썬강좌
- 백준 알고리즘
- c언어 오목
- unsupervised learning
- 자바시작하기
- feature scaling
- 딥러닝
- acmicpc.net
- 머신러닝 강의
- 자바
- 머신러닝공부
- 지도학습
- 머신러닝 강좌
- java
- 비지도학습
- 효묘블로그
- JAVA강좌
- Today
- Total
컴공과컴맹효묘의블로그
수알못의 머신러닝 공부 : 경사하강법 본문
저번 시간에는 비용함수에 대해서 공부했습니다.
다시 정리하지면, 비용함수는 "오차를 표현해주는 미분 가능한 함수" 입니다.
비용함수가 오차들의(제곱의)평균이므로 오차의 최소값을 구해야겠죠? 실제로 최소값(global minimum)을 구하는 것은 어려우니, 경사하강법으로 극소값(local minimum)을 구할 수 있습니다.
따라서 경사하강법은 비용함수의 극소값을 구하는 방법입니다.
경사하강법 Gradient descent
경사하강법은 특정한 점 x를 잡고, 비용함수의 기울기를 구한 후, 기울기에 따라서 x의 값을 변화시켜주는 방법입니다.
그림으로 쉽게 설명하겠습니다.
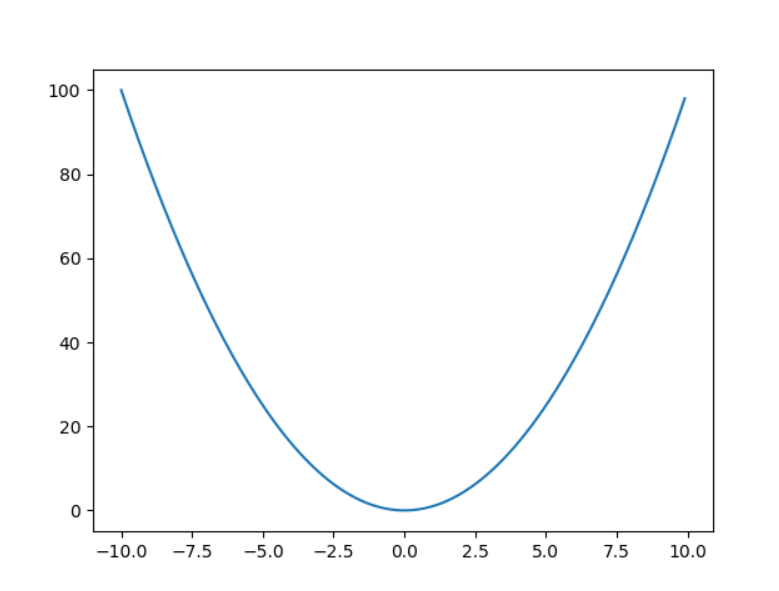
여기 단순한 y=x^2의 그래프가 있습니다.
그리고 이 그래프의 아무점, 예를들어서 7.5를 잡아본다고 하겠습니다.
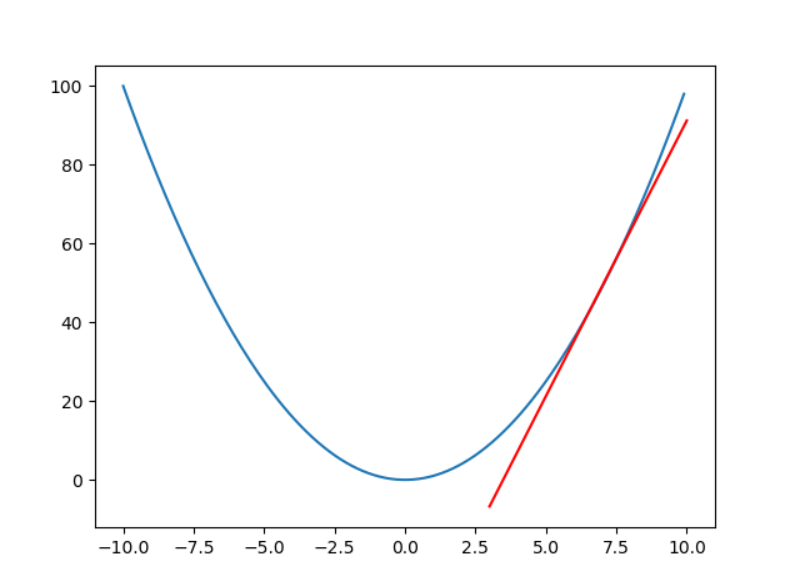
x = 7.5일 때, 접선은 다음과 같습니다.
이때의 접선의 기울기는 '양수'입니다.
반면, x = -7.5일때의 접선을 보겠습니다.
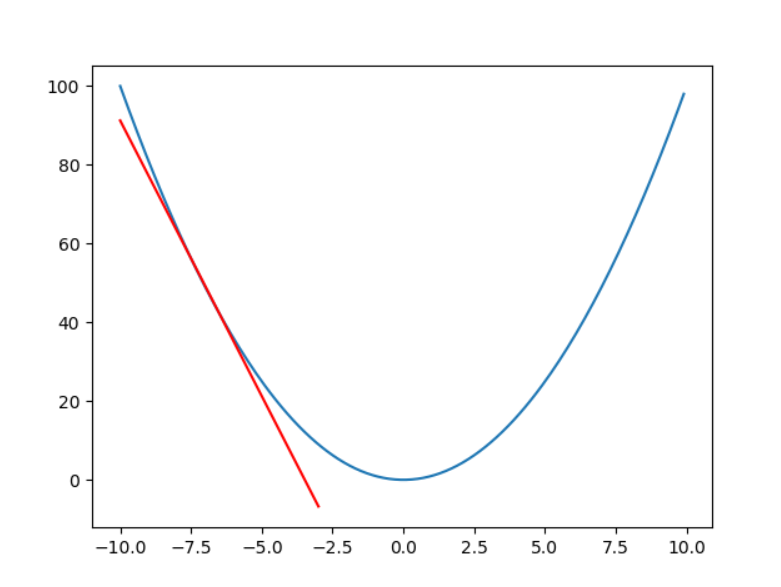
이때의 기울기는 '음수'입니다.
왜 양수인지 음수인지 중요한지는 다음 수식을 보면 알 수 있습니다.
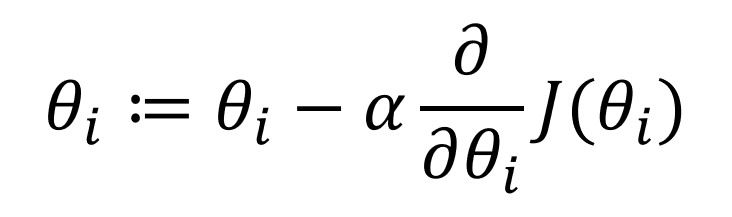
이 수식은 비용함수의 매개변수인 세타값의 갱신(update) 수식입니다.
:=의 의미는 좌측의 연산값을 우측으로 대입한다는 뜻입니다. 프로그래밍을 조금이라도 해보셨다면 바로 이해가 가실겁니다.
잠시 알파 옆의 6을 뒤집어놓은 듯한 문자에 대해 설명드리겠습니다. 저 기호는 '라운드'라고 읽습니다. 고등학생이라면, 미분을 배웠을겁니다. 델타y, 델타x 이처럼 라운드도 미분이지만, 조금 다른 편미분이라고 하는 것입니다. 편미분은 그리 어려운 개념이 아닙니다. 편미분이란, 미분하고싶은 매개변수를 제외하고, 모든 매개변수를 상수취급 한다는 의미입니다.
이 때 알파는 학습률(learning rate)를 뜻하고, '상수'입니다. 학습률에 대해서는 뒷 부분에서 이야기 하겠습니다.
비용함수의 편미분값이 양수라면, 세타의 값은 작아지고,
비용함수의 편미분값이 음수라면, 세타의 값은 커집니다.
따라서 결국, 위 수식을 반복하다보면 결국에는 극소값에 다다를 수 있습니다.
하지만 주의할 점이 있습니다. 바로 학습률의 크기인데요, 학습률이 너무 크면 over shoot이 될 수 있고, 너무 작다면, 극소값을 구하기 까지가 너무 오래걸릴 것입니다.
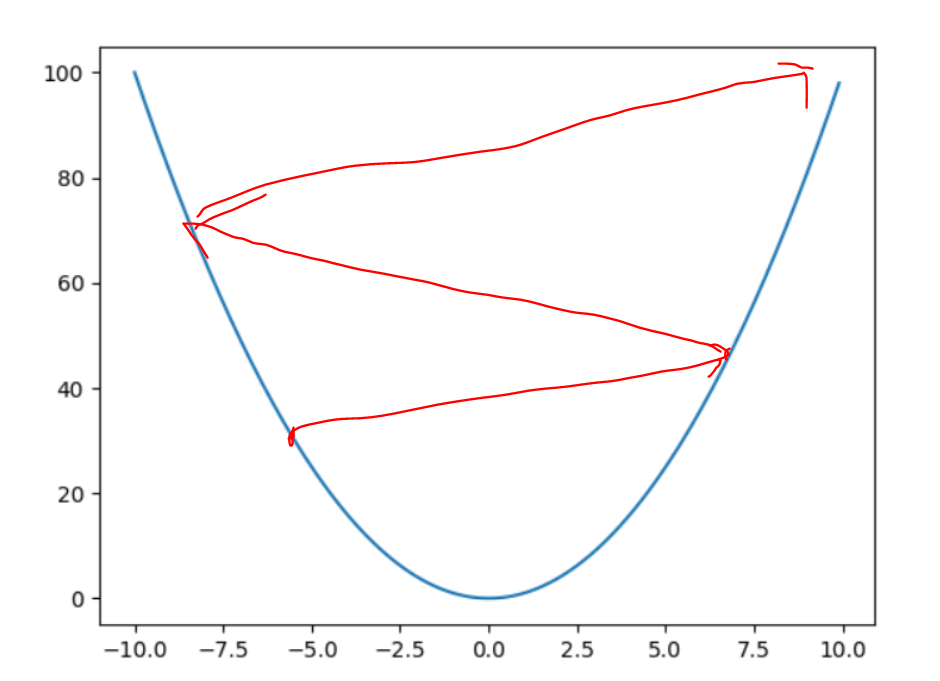
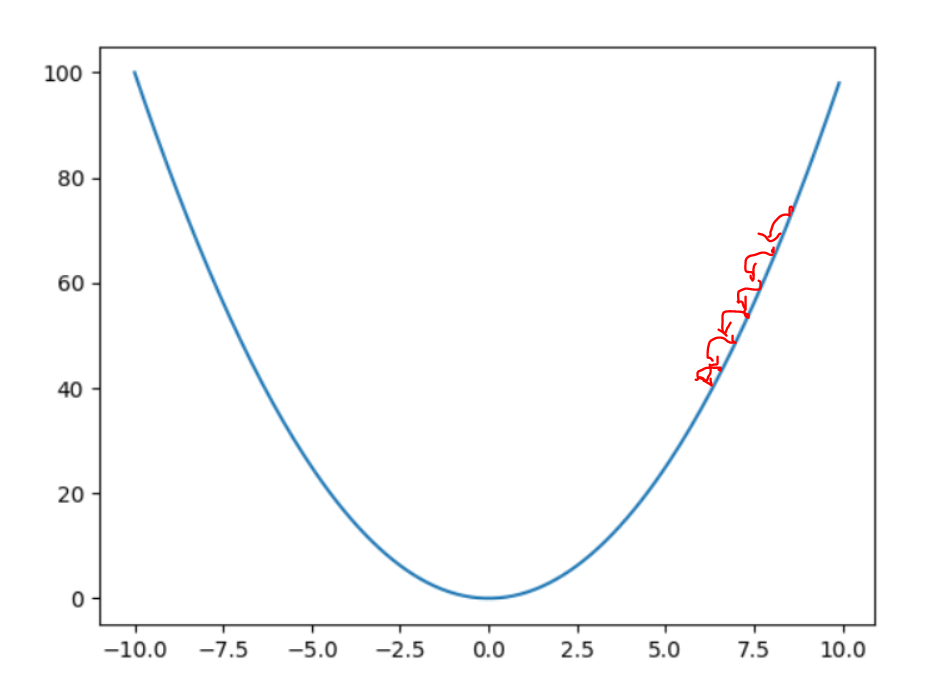
그렇다면 학습률은 몇으로 해야할까? 적당히 작은 값으로 하면 된다.
위 그래프인경우엔, a = 1e-5정도로 초기화해주면 프로그램에서 잘 작동할 것입니다.
그렇다면 또다른 의문이 생길 수 있습니다. 만약 학습률이 상수라면, 그리고 세타의 값이 만약 극소값 주변에서 맴돌 수 있지 않을까? 라는 의문입니다. 물론 그럴 수 있지만, 이 문제는 더 작은 학습률을 적용시키면 해결이 됩니다. 그리고 세타는 기울기의 방향 뿐만 아니라 기울기의 값도 영향을 받습니다.
예를 들어서 기울기가 100이라면, 세타의 값은 많이 작아질 것이고, 기울기가 0.01이라면 세타의 값은 조금 작아질 것입니다.
theta := theta - a * 100
theta := theta - a * 0.01
이렇게 되면 세타가 극소값에 가까워질수록 변화량이 작아지고, 결국에는 극소값에 수렴할 수 있습니다.
실제로는 극소값이 여러 개일 것입니다. 그 여러 개의 극소값중, 너무 큰 극소값도 있을 것이고, 최소값에 해당하는 극소값도 있을 것입니다. 이 문제는 그저, theta의 초기값을 랜덤으로 변경해주면서 여러번 학습할 수 밖에 없습니다.
정리 : 비용함수의 매개변수 갱신 수식
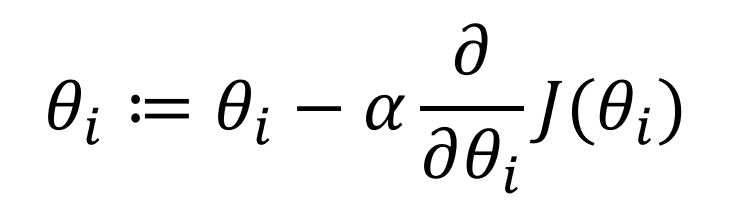
'컴퓨터 > 머신러닝' 카테고리의 다른 글
| 수알못의 머신러닝 공부 : 행렬과 벡터_행렬곱 (0) | 2019.06.27 |
|---|---|
| 수알못의 머신러닝 공부 : 행렬과 벡터_표현 (0) | 2019.06.25 |
| 수알못의 머신러닝 공부 : 경사하강법 Python으로 구현해보기 (0) | 2019.06.18 |
| 수알못의 머신러닝 공부 : 비용함수 (2) | 2019.06.16 |
| 머신러닝 기초 : 머신러닝이란? (0) | 2019.06.16 |





