| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 딥러닝
- 자바
- 파이썬강좌
- 비용함수
- 자바강좌
- 파이썬강의
- acmicpc.net
- Gradient Descent
- 머신러닝
- supervised learning
- unsupervised learning
- java
- 지도학습
- 인공지능
- 머신러닝공부
- 자바시작하기
- 경사하강법
- 딥러닝공부
- Python강의
- 코딩테스트
- 선형회귀
- python강좌
- 머신러닝 강의
- c언어 오목
- feature scaling
- 비지도학습
- JAVA강좌
- 머신러닝 강좌
- 효묘블로그
- 백준 알고리즘
- Today
- Total
컴공과컴맹효묘의블로그
수알못의 머신러닝 공부 : Logistic Regression을 이용한 Classification을 Python으로 구현 본문
개인적인 공부 기록용 포스팅입니다. 따라서 이해가 어려운 부분이 있을 수 있습니다. 하지만 질문이나 지적할 점이 있다면 댓글 써주시면 최대한 이해하시기 쉽게 답변해드리도록 하겠습니다.
저번엔 x의 input 종류가 1개인 간단한 Linear regression을 python으로 구현했었습니다.
수알못의 머신러닝 공부 : 경사하강법 Python으로 구현해보기
지금까지 공부한 선형회귀를 수식적으로 표현한 후에 Python으로 구현해볼려고 합니다. 아래의 수식들은 이전 포스팅에서 자세히 다뤘습니다. 바로가기 수알못의 머신러닝 공부 : 비용함수 수알못의 머신러닝 공부..
hyomyo.tistory.com
이번에는 logistic regression을 공부하고 python으로 구현을 해보았습니다.
logistic은 분류 모델을 구현할 때 많이 쓰이는 모델입니다.
x의 input 종류 개수는 feature의 개수라고 하겠습니다. 이번에는 코드 일부를 일반화 시켜서 feature의 개수가 몇 개인지 상관 없이 코드를 구현했습니다.
이전 output값의 hypothesis 함수는 값이 너무 커질 수도 있다는 점이 문제였습니다. 값이 너무 커져버리면 오차의 최소도 너무 커져버릴 수도 있다는 문제점이 있었습니다.
D. R. Cox는 이러한 문제를 해결하려고 logistic regression model을 제안했습니다. logistic regression과 linear regression 모델의 핵심적인 차이점은 모델의 output값(이하 hypothesis)의 정의가 바뀌었다는 점입니다.
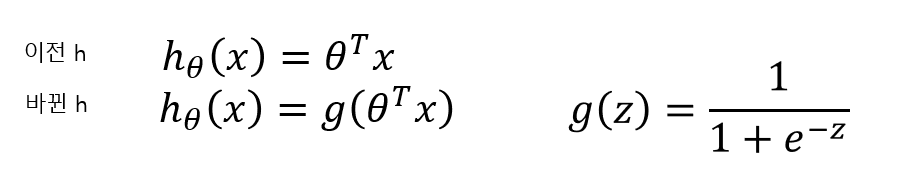
g함수는 logistic function이라고 불리고, sigmoid function라도고 불립니다.
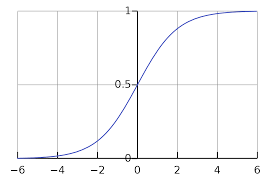
위 사진처럼 sigmoid 함수는 0과 1사이의 값을 가집니다. 이것은 확률을 나타낼겁니다. 어떤 x값에 대해서 y가 1이 나와야 하는 경우 h(x)는 hypothesis의 값이 1일 확률을 나타냅니다.
반대로 어떤 x값에 대해서 y가 0이 나와야 하는 경우 h(x)는 hypothesis의 값이 0일 확률을 나타냅니다.
그리고 저는 Classification(분류) 모델을 구현 할것이기 때문에 y의 dataset은 0과 1로만 이루어져 있다고 하겠습니다.
비용함수를 오차제곱함수로 정의하면, linear하지 않은 logistic function때문에 이 비용함수가 울퉁불퉁하게 될 수 있습니다. 그렇게 되면 비용함수의 최소값을 찾지 못하고(global minimun) 극소값을 찾을 수도 있습니다.(global minimun) 따라서 비용함수를 재정의 할 필요가 있습니다.
비용함수는 다음과 같습니다.

y=1일 경우 위 그래프를 따릅니다. h(x)의 값이 1에 가까워질수록 비용함수는 0에 가까워지므로 h(x)가 1일 때 가장 최적인 경우를 볼 수 있습니다.
y=0인 경우도 그래프를 그려보면 쉽게 이해가 갈겁니다.
세타의 업데이트를 위해 경사하강법을 적용하여 이 비용함수를 미분하면 정말 간단한 값이 나옵니다.
동시에 세타와 x를 vector(cloumn vector)로 표현하겠습니다.
m is number of training set
update theta simultaneously

Python code
아직 파이썬이 익숙치 않아 코드가 많이 더럽습니다..
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x));
n = 2 # features of x
m = 1000 #학습 데이터 개수
half_m = int(m/2)
x1_data = np.array((np.random.normal(0.5, 0.3, half_m), np.random.normal(-0.5, 0.3, half_m)))
x1_data = np.resize(x1_data, m)
x2_data = np.array((np.random.normal(-0.5, 0.3, half_m), np.random.normal(0.5, 0.3, half_m)))
x2_data = np.resize(x2_data, m)
y_data = np.array((np.ones(half_m), np.zeros(half_m)))
y_data = np.resize(y_data, m)
theta = np.random.normal(0.0, 0.5, n+1).T
iteration = 100
learning_rate = 0.03
for _ in range(iteration):
gamma = np.zeros(n+1).T
for i in range(m):
x = np.array((1, x1_data[i], x2_data[i]))
x = np.resize(x, n+1).T
gamma += (sigmoid(theta.T@x)-y_data[i])*x
theta-=learning_rate*gamma
tmpX = np.arange(-1, 1, 0.1)
tmpY = (theta[0] + theta[1]*tmpX)/theta[1]
print(tmpX)
plt.plot(x1_data[0:half_m], x2_data[0:half_m], 'r.')
plt.plot(x1_data[half_m:], x2_data[half_m:], 'b.')
plt.plot(tmpX, tmpY)
plt.show()
결과 화면

'컴퓨터 > 머신러닝' 카테고리의 다른 글
| DBSCAN을 이용한 식당 리뷰 요약 서비스 (6) | 2025.06.08 |
|---|---|
| k-means 알고리즘 python으로 구현해보기 (2차원 데이터 시각화) (0) | 2020.04.25 |
| 수알못의 머신러닝 : 선형회귀 - normal equation 정규방정식 (0) | 2019.08.23 |
| Polynomail Regression 다항식 회귀 (0) | 2019.08.19 |
| 머신러닝 회귀 분석 Feature Scaling (0) | 2019.08.19 |




